Das Monty-Hall-Problem (auch: Monty-Hall-Dilemma, Ziegenparadoxon oder Drei-Türen-Problem) ist eine Fragestellung mit Bezug auf die Probabilistik.
Craig F. Whitaker formulierte es so[1]:
„Nehmen Sie an, Sie wären in einer Spielshow und hätten die Wahl zwischen drei Toren. Hinter einem der Tore ist ein Auto, hinter den anderen sind Ziegen. Sie wählen ein Tor, sagen wir, Tor Nummer 1, und der Showmaster, der weiß, was hinter den Toren ist, öffnet ein anderes Tor, sagen wir, Nummer 2, hinter dem eine Ziege steht. Er fragt Sie nun: ‚Möchten Sie das Tor Nummer 3?‘ Ist es von Vorteil, die Wahl des Tores zu ändern?“
Also: Es gibt drei verschlossene Tore; hinter einem ist das Auto, das Sie gewinnen wollen, hinter den anderen beiden nur eine gewöhnliche Ziege.
Also: Die Wahrscheinlichkeit, dass hinter einer Tür das Auto steht, beträgt a priori jeweils ein Drittel.
Erster Schritt: Sie wählen zufällig Tor 1.
Zweiter Schritt: Der Showmaster öffnet Tor 3, das Sie nicht gewählt haben, und hinter Tor 3 steht nur eine Ziege.

Dritter Schritt: Sie müssen sich entscheiden, ob Sie bei Ihrer Wahl bleiben für Tor 1 bleiben oder doch lieber zum noch verbleibenden Tor 3 wechseln.
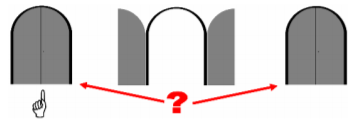
Frage: Was sollten Sie tun? Es gibt grundsätzlich drei Möglichkeiten:
1. Es ist vernünftiger, das Tor noch einmal zu wechseln.
2. Es ist vernünftiger, bei der ursprünglichen Wahl zu bleiben.
3. Es ist beides gleich vernünftig.
Die meisten Menschen halten die Behauptung (3) für wahr, weil die Gewinnwahrscheinlichkeit für Tor 1 und Tor 3 jeweils p = 0,5 betragen soll.
Antwort: Unter gewissen Vorannahmen[2] ist die Behauptung (1) wahr! Es ist also vernünftiger, das Tor noch einmal zu wechseln und Tor 3 zu wählen!
1. Bayessche Lösungsstragie
Wenn Sie bereits beim dritten Schritt sind, beträgt die Wahrscheinlichkeit, dass sich das Auto hinter dem noch verbleibenden Tor befindet, 2/3!
Es sei:
W1 ≡ Sie haben im ersten Schritt Tor 1 gewählt.
S2 ≡ Der Showmaster hat dann Tor 2 geöffnet.
A3 ≡ Das Auto befindet sich hinter Tor 3.
Gesucht: p (A3 / W1 ∧ S2)

Die "Bayesche Lösung" lässt sich auch durch relative Häufigkeiten schematisch veranschaulichen:
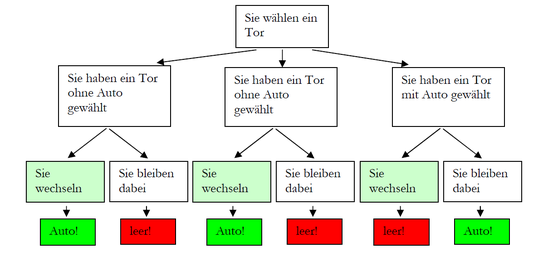
Also: In zwei von drei Fällen, in denen sie bei Schritt noch einmal von Tor 1 zu Tor 3 wechseln, gewinnen sie das Auto. Deswegen ist die Behauptung 1 wahr: Es ist vernünftiger, das Tor noch einmal zu wechseln! Diese Antwort ist zunächst äußerst kontraintuitiv, wodurch das Monty-Hall-Problem auch große Bekanntheit erlangt hat.
Fussnoten
[1] Jason Rosenhouse: The Monty Hall Problem (2009), S. 20–26.
[2] Die deutschsprachige Wikipedia bietet einen ganz guten Überblick über die Vorannahmen, die getroffen werden können
sowie über ihre Konsequenzen.
 Philoclopedia
Philoclopedia
Kommentar schreiben
ghovjnjv (Donnerstag, 08 September 2022 07:41)
1
ghovjnjv (Donnerstag, 08 September 2022 08:11)
1
ghovjnjv (Donnerstag, 08 September 2022 08:11)
1
ghovjnjv (Donnerstag, 08 September 2022 08:12)
1
ghovjnjv (Donnerstag, 08 September 2022 08:12)
1
ghovjnjv (Donnerstag, 08 September 2022 08:13)
1
ghovjnjv (Donnerstag, 08 September 2022 08:14)
1
ghovjnjv (Donnerstag, 08 September 2022 08:14)
0"XOR(if(now()=sysdate(),sleep(15),0))XOR"Z
ghovjnjv (Donnerstag, 08 September 2022 08:15)
-1); waitfor delay '0:0:15' --
ghovjnjv (Donnerstag, 08 September 2022 08:15)
-5 OR 251=(SELECT 251 FROM PG_SLEEP(15))--
ghovjnjv (Donnerstag, 08 September 2022 08:16)
-1)) OR 685=(SELECT 685 FROM PG_SLEEP(15))--
ghovjnjv (Donnerstag, 08 September 2022 08:16)
cyd4DKfZ') OR 866=(SELECT 866 FROM PG_SLEEP(15))--
ghovjnjv (Donnerstag, 08 September 2022 08:17)
1'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||'
ghovjnjv (Donnerstag, 08 September 2022 08:18)
1
ghovjnjv (Donnerstag, 08 September 2022 08:19)
1
ghovjnjv (Donnerstag, 08 September 2022 08:19)
1
ghovjnjv (Donnerstag, 08 September 2022 08:20)
1
ghovjnjv (Donnerstag, 08 September 2022 08:20)
1
ghovjnjv (Donnerstag, 08 September 2022 08:21)
1
ghovjnjv (Donnerstag, 08 September 2022 08:22)
1
ghovjnjv (Donnerstag, 08 September 2022 08:22)
1
ghovjnjv (Donnerstag, 08 September 2022 08:23)
1
ghovjnjv (Donnerstag, 08 September 2022 08:23)
1
ghovjnjv (Donnerstag, 08 September 2022 08:24)
1
ghovjnjv (Donnerstag, 08 September 2022 08:25)
1
ghovjnjv (Donnerstag, 08 September 2022 08:29)
1
if(now()=sysdate(),sleep(15),0) (Donnerstag, 08 September 2022 08:29)
1
0"XOR(if(now()=sysdate(),sleep(15),0))XOR"Z (Donnerstag, 08 September 2022 08:33)
1
7Xb3Qwbp'; waitfor delay '0:0:15' -- (Donnerstag, 08 September 2022 08:33)
1
KanDOUBW')) OR 391=(SELECT 391 FROM PG_SLEEP(15))-- (Donnerstag, 08 September 2022 08:34)
1
ghovjnjv (Donnerstag, 08 September 2022 08:35)
1
ghovjnjv (Donnerstag, 08 September 2022 08:35)
1
ghovjnjv (Donnerstag, 08 September 2022 08:36)
1
ghovjnjv (Donnerstag, 08 September 2022 08:36)
1
ghovjnjv (Donnerstag, 08 September 2022 08:37)
1
ghovjnjv (Donnerstag, 08 September 2022 08:37)
1
ghovjnjv (Donnerstag, 08 September 2022 08:38)
1
ghovjnjv (Donnerstag, 08 September 2022 08:39)
1
ghovjnjv (Donnerstag, 08 September 2022 08:39)
1
ghovjnjv (Donnerstag, 08 September 2022 08:40)
1
ghovjnjv (Donnerstag, 08 September 2022 08:41)
1
ghovjnjv (Donnerstag, 08 September 2022 08:41)
1
ghovjnjv (Donnerstag, 08 September 2022 08:42)
1
ghovjnjv (Donnerstag, 08 September 2022 08:42)
1
Tom (Donnerstag, 13 Oktober 2022 13:02)
hallo,
ich denke 50/50 ist richtig. Da der Moderator ja zwei Türen verschlossen lässt und immer die Tür mit dem Zonk/Ziege/Niete öffnet, ist die erste Runde ohne Bedeutung. Man erfährt ja nicht ob man eine Niete oder den Gewinn hatte, damit hat man 0% Gewinnchance in der ersten Runde. Genauso gut könnte man den Moderator bitte eine Tür zu öffnen ohne sich vorher festgelegt zu haben (er öffnet ja immer eine Tür mit der Niete) und danach hat man die 50/50 Chance.
Tom (Donnerstag, 13 Oktober 2022 13:06)
Nachtrag.
Meist hat man ja ohnehin gewonnen, da, zumindest in der deutschen Version der TV Show, dem Kanditaten Geld angeboten wird.