Dieser Artikel behandelt das Bellsche Theorem des Physikers John Stewart Bell.
1. Einleitung
Die Diskussion um die Bellsche Ungleichung nimmt ihren Ausgangspunkt bei der Beschreibung von zusammengesetzten Systemen in der Quantentheorie.
Ein Beispiel für so ein System ist eines aus zwei Atomen. Ein solches System kann nun einerseits über Produktzustände beschrieben werden wie z.B. so:
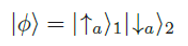
Diese mathematische Formel beschreibt ein aus zwei Systemen zusammengesetztes Gesamtsystem. Dabei kennzeichnen die Indizes "1" und "2" welchem System der Zustand in der Klammer zukommt. "|↑a⟩1" besagt z.B., dass das System 1 den Zustand "Spin up" bzgl. der räumlichen Richtung a besitzt. Und "|↓a⟩2" besagt dementsprechend, dass das System 2 den Zustand "Spin down" bzgl. der räumlichen Richtung a besitzt. Angenommen also die Formel beschreibt ein System aus zwei Protonen. Dann sagt sie als Ganzes aus, dass das Proton 1 die Eigenschaft "Spin up" und dass das Proton 2 "Spin down" bezüglich a hat.
In den meisten Fällen kann man zusammengesetzte Systeme aber nicht durch Produktzustände, sondern nur durch die Superposition von Produktzuständen beschreiben. Das heißt durch sogenannte verschränkte Zustände wie z.B. so:
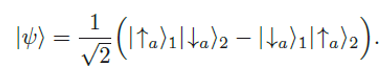
Die mathematische Formel oben beschreibt den berühmten Singulett-Zustand. Die Indizes "1" und "2" legen mathematisch nahe, dass es sich hierbei um den Zustand eines Gesamtsystems handelt, das aus zwei Teilsystemen zusammengesetzt ist. Die Formel (2) kann anders als die Formel (1) jedoch nicht in Produktform gebracht werden. Dies bedeutet, dass mathematisch weder dem System 1 noch dem System 2 ein eindeutiger Spinzustand zugeordnet werden kann. Mit anderen Worten: Die Beschreibung des Gesamtzustandes durch "|Ψ⟩" legt nicht die jeweiligen Spinzustände der einzelnen Teilsysteme 1 und 2 fest.
Wenn man aber Spinmessungen an den Teilsystemen durchführt, erhält man für jedes der Systeme 1 und 2 jeweils eindeutige Messergebnisse. Diese sind zwar zufällig verteilt, es gibt aber gewisse Korrelationen zwischen den Messergebnissen: Wenn man für System 1 den Zustand |↑a⟩1 misst, liegt nach der Messung am System 2 mit Sicherheit der Zustand |↓a⟩2 vor und vice versa. Nach der Quantentheorie sind diese Korrelationen unabhängig von der räumlichen Entfernung der Teilsysteme 1 und 2. Insbesondere liegen sie auch dann vor, wenn 1 und 2 raumartig voneinander entfernt sind, d.h. wenn kein Signal zwischen diesen Systemen mit Lichtgeschwindigkeit diese Korrelationen herstellen könnte.
Die Verschränkung von Systemen spielt eine große Rolle bei fast allen zentralen Probleme der Interpretation der Quantentheorie. Siehe z.B. das ontologische Problem oder das Messproblem. Sie widerspricht darüber hinaus fundamentalen Prinzipien der klassischen Physik und steht im Spannungsver-hältnis mit der speziellen Relativitätstheorie. Erwin Schrödinger hat dieses Phänomen als das zentrale Charakteristikum der Quantentheorie bezeichnet.
2. Das EPR-Argument
Das EPR-Argument wurde 1935 von Albert Einstein, Boris Podolsky und Nathan Rosen entwickelt und ist nach diesen benannt. Es wurde ursprünglich mit einer Wellenfunktion und in Bezug auf Ort und Impuls formuliert. Seit den 1950er Jahren wird das Argument aber vor allem in Bezug auf ein Lehrbuchbeispiel des Physikers David Bohm diskutiert. Die zugehörige Formel kennen wir bereits:
Messungen an verschränkten Systemen und mit einem raumzeitlichen Aufbau wie im ursprünglichen EPR-Argument heißen EPR/B-Experimente. Das EPR-Argument besagt nun, dass nach der Quantentheorie und aufgrund der Messkorrelationen eine Messung am System 1 den entsprechenden Zustand des Systems 2 festlegt und vice versa. Dies ist nach EPR aber unmöglich, da es keine physikalische Wechselwirkung zwischen den Systemen 1 und 2 geben kann. Die Systeme 1 und 2 müssen also schon vor der Messung definitive numerische Spinwerte besitzen. Diese werden im mathematischen Formalismus der Quantentheorie aber nicht abgebildet. Daraus schlussfolgerten EPR, dass die Quantentheorie eine unvollständig wissenschaftliche Theorie sei.
Diese Schlussfolgerung kann mathematisch wie folgt gestützt werden: Der Spinzustand des oben beschriebenen Gesamtsystems wird durch einen Zustands-vektor im Hilbertraum des Tensorprodukts H1⊗H2 dargestellt, der aus den Spin-Hilberträumen der Teilsysteme gebildet wird. |↑a⟩1 ist im Spinraum des Teilchens 1 der Eigenvektor des Operators Ŝz1 zum Eigenwert +ħ/2 und |↓a⟩1 der Eigenvektor zum Eigenwert -ħ/2. Ŝz1 ist der Operator zur Observablen "Spinprojektion in a-Richtung". Ebenso ist für das zweite System |↑a⟩2 der Eigenvektor des Operators Ŝz1 zum Eigenwert +ħ/2 und |↓a⟩2 der Eigenvektor zum Eigenwert – ħ/2. Die Eigenvektoren bilden jeweils ein vollständiges System von Basisvektoren in den Spinräumen der einzelnen Teilchen. Die Vektoren |↑a⟩1 |↑a⟩2, |↑a⟩1|↓a⟩2, |↓a⟩1|↑a⟩2, und |↓a⟩1|↓a⟩2 bilden eine vollständige Basis im Hilbertraum des Tensorprodukts. Kehren wir nun zum Singulett-Zustand zurück. Dieser Zustandsvektor ist gemeinsamer Eigenvektor zu den Spinprojektionsoperatoren Ŝx, Ŝy und Ŝz des Gesamtsystems, obwohl diese Operatoren nicht kommutieren. Man kann ihn auch wie folgt aufschreiben:
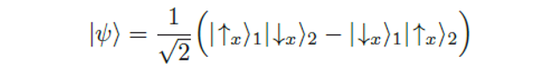
Es lässt sich anschaulich auch sagen, dass der Singulett-Zustand rotationssymmetrisch zur Achse ist, in der sich die Teilchen voneinander entfernen. Der in (3) beschriebene Zustand ist Eigenvektor des Gesamtspins:
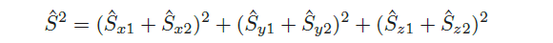
Ŝz und Ŝ2 bilden ein maximales System von kommutierenden Operatoren für diesen Zustand. Das heißt man kann dem System in diesem Zustand maximal den Wert (die Eigenschaft) des Gesamtspins (hier 0) und gleichzeitig den Wert (die Eigenschaft) der Spinprojektion in z-Richtung (hier auch 0) zuordnen. Der in (3) beschriebene Zustand ist allerdings kein Eigenzustand zu dem Operator Ŝz1⊗ I, der auf dem gesamten Spinraum dadurch definiert ist, dass Ŝz wie Ŝz1 auf den ersten Faktor der Basisvektoren im Produktraum wirkt und der zweite Faktor unverändert bleibt. Den einzelnen Teilchen kann also kein Eigenwert des Operators Ŝz1 und damit keine definierte Größe der Spinprojektion zugeordnet werden. Dem entspricht anschaulich, dass der Zustandsvektor der einzelnen Teilchen nicht durch einen reinen Zustand charakterisiert werden kann.
Das ist erst einmal ein mathematischer Sachverhalt. Man kann unterschiedlich mit ihm umgehen. Wenn man selbst im verschränkten Singulett-Zustand an der Vorstellung festhalten möchte, dass beide Systeme je durch einen Zustand charakterisiert werden, kann man das nur durch den statistischen Operator:
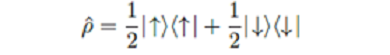
Die beiden Systeme 1 und 2 werden hier durch sog. "gemischte Zustände" beschrieben. Allerdings kann man aus diesen Zuständen nicht die Korrelationen zwischen den Messungen an den Systemen 1 und 2 bestimmen. Deshalb wird auch gesagt, dass der Gesamtzustand nicht durch die Zustände der Teilsysteme festgelegt wird. In diesem Fall sind die Dichte-Operatoren für 1 und 2 sogar gleich, weswegen einige Autoren argumentieren, dass hier das Leibniz-Prinzip verletzt ist. Gegen diese Autoren lässt sich aber einwenden, dass der mathematische Apparat eher nahelegt, dass in einem Singulett-Zustand gar nicht von Zuständen oder Eigenschaften der Teilsysteme gesprochen werden kann.
Bei einer Messung liegen die Systeme aber in sog. "reinen Zuständen" vor. Nach dem Formalismus der Quantentheorie ist sogar zu erwarten, dass nach der Messung an nur einem System beide in reinen Zuständen vorliegen. Die Messergebnisse sind dabei korreliert: Wenn man beispielsweise für System 1 Spin-up misst, dann misst man für System 2 Spin down und vice versa. Das Messergebnisse an einem Zustand wie beschrieben in (2) beträgt also immer entweder |↑a⟩1|↓a⟩2 oder |↓a⟩1|↑a⟩2. Aufgrund der Rotationssymmetrie der Messungen kann man diese Korrelationen in beliebigen Spinrichtungen finden.
Das bisher Gesagte zeigt, weshalb es u.a. so schwer ist, eine Ontologie der Quantentheorie auszuformulieren. Mit anderen Worten: Es ist schwierig zu sagen, auf welche Ontologie man festgelegt ist, wenn man die Quantentheorie (oder eine bestimmte Interpretation von ihr) für wahr oder annähernd wahr hält. Denn in einem verschränkten Zustand ist es nicht möglich, Teilsystemen bestimmte Eigenwerte und Eigenvektoren, das heißt bestimmte Eigenschaften zuzuschreiben. Deshalb ist unklar, ob und wenn ja in welchem Sinne man überhaupt von Teilsystemen sprechen kann. Viele Autoren vertreten hier einen ontischen Strukturenrealismus, nach dem die Teilsysteme ihre Eigenschaften nur in Relation zu den anderen Systemen haben. Das ist eine revolutionäre Ontologie! Denn nach ihr scheint es gar keine Objekte mit intrinsischen Eigenschaften sondern nur noch relationale Eigenschaften und in Folge auch gar keine Objekte sondern nur noch Strukturen im Sinne von Relationen zu geben.
3. Das Bellsche Theorem
Das Bell-Theorem des nordischen Physikers John Stewart Bell hat dem EPR-Argument eine ganz neue Wendung gegeben. Bell konnte in einer bahnbrechenden Arbeit von 1964 zeigen, dass pace Einstein die EPR-Korrelationen nicht durch lokale verborgene Parameter im mathematischen Formalismus der Quantentheorie erklärt werden können. Etwas genauer können die EPR-Korrelationen selbst dann nicht durch lokale Prozesse erklärt werden, wenn man verborgene Variablen annimmt. Denn die Annahme von verborgenen Parametern, welche eine allgemein statistisch formulierte Lokalitätsbedingung erfüllen, wie Einstein das im Sinn hatte, reichen nicht aus, um die starken Korrelationen zwischen den Messergebnissen zu erklären. Es muss wohl als eine Ironie der Geschichte betrachtet werden, dass gerade Einsteins Überlegungen eine Debatte initiiert haben, die zu der Erkenntnis führten, dass die Quantenwelt in einem gehaltvollen und überraschenden Sinne in jedem Fall nicht-lokal ist!
Bells Theorem hat somit dazu geführt, dass die EPR-Korrelationen nicht mehr als ein Argument für die Unvollständigkeit der Quantenmechanik gewertet werden. Stattdessen ist man mehrheitlich der Meinung, dass der zigfache experimentelle Nachweis dieser Korrelationen eine große Klasse von Theorien mit verborgenen lokalen Parametern ausschließt. Mit anderen Worten: Jede korrekte gegenwärtige und zukünftige Theorie der Mikrowelt muss zwangsläufig eine bestimmte Nicht-Lokalität beinhalten. Die Debatte hat sich damit weg von der vermeintlichen Unvollständigkeit der Quantentheorie hin zu der Frage nach der genaueren Bedeutung der Nicht-Lokalität in der Quantentheorie verschoben, welche sich in den korrekt vorhergesagten EPR-Korrelationen zeigt.
Dieser Abschnitt beinhaltet eine systematische Auseinandersetzung mit Bells Theorem. Es werden dabei die experimentellen Grundlagen, impliziten Voraus-setzungen, präzise Ausformulierung und Konsequenzen des Theorems diskutiert.
3.1. experimentelle Grundlagen
Die Experimente, die Bells Theorem zugrunde liegen, sind Realisierungen der EPR/B-Experimente. In ihren modernsten Varianten werden diese Experimente mit Photonen durchgeführt. Das Experiment läuft typischerweise wie folgt ab: Eine Quelle C wird dazu angeregt, ein Photonenpaar zu emittieren, dessen Polarisationszustände verschränkt sind. Der Gesamtzustand wird so beschrieben:
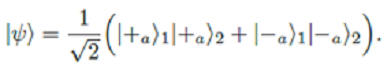
Hierbei steht |+a⟩1 für eine Polarisation in Richtung a und |-a⟩1 repräsentiert eine Polarisation senkrecht zu a. Die einzelnen Photonen haben auch in diesem Zustand keine numerisch definite Polarisation. Nach der Emission durch die Quelle bewegen sich die Photonen in entgegengesetzten Richtungen auf zwei Messgeräte A und B zu. Jedes der Messgeräte hat einen Zeiger, mit dem man die Richtung a oder b einstellen kann, in der die Polarisation gemessen wird. Diese Messrichtung wird zufällig aus einem von drei möglichen Winkeln ausgewählt. Die Auswahl und Einstellung der Richtung kann nach der Emission der Photonen vorgenommen werden. Somit wird sichergestellt, dass sie keinen Einfluss auf die Ergebnisse hat.
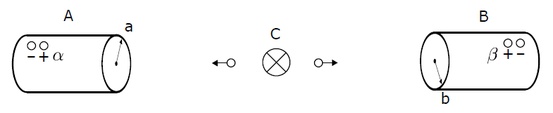
Wenn ein Photon auf das Messgerät trifft, detektiert dieses ob das Photon in die eingestellte Richtung oder senkrecht zu dieser polarisiert ist. Es gibt für jedes Messgerät also zwei mögliche Messergebnisse α = ± respektive β = ±. Ein kompletter Durchgang des Experiments wird folglich durch fünf Variablen bestimmt: Die Präparation der Quelle C, die zwei Messeinstellungen a und b und die zwei Messergebnisse an A und B. Ein typisches Laborprotokoll für ein EPR/B-Experiment sieht dementsprechend wie in Tabelle 1 unten aus:
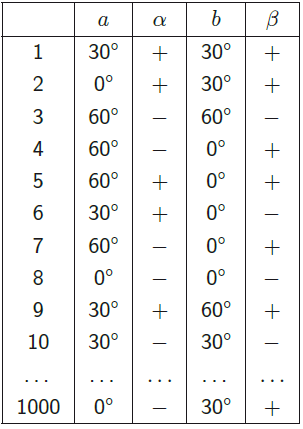
Diese harmlos aussehende Zahlenreihe hat es in sich. Alle weitreichenden Konsequenzen, die mithilfe von Bells Theorem gezogen werden – Nicht-Lokalität, Nicht-Separabilität, Holismus, spukhafte Fernwirkungen etc. – basieren auf solchen einfachen Daten, die aus EPR/B-Experimenten gewonnen werden.
Einen ersten Hinweis auf die Besonderheit der Daten erhält man, wenn man selbige statistisch auswertet. Es ergeben sich drei Typen von Korrelationen:
1. Perfekte Korrelation: Wenn die Winkel der Messgeräte gleich sind (vgl. Durchgang
1,3,8,10, ...), stimmen die Ergebnisse in 100% der Fälle überein.
2. Nicht-perfekte Korrelation1: Wenn die Winkel der Messgeräte um 30° differieren (vgl. Durchgang 2,6,9, ... , 1000), stimmen die Ergebnisse in 75% der Fälle überein.
3. Nicht-perfekte Korrelation2: Wenn die Winkel der Messgeräte um 60° differieren (vgl. Durchgang 4,5,7, ...), stimmen die Messergebnisse in 25% der Fälle überein.
Die Korrelationen zwischen den Messwerten in Tabelle 1 sind unerwartet stark und ihre Stärke hängt nur vom relativen Winkel zwischen den Messrichtungen ab. Das ist aus dem Grund unerwartet, weil der Aufbau der EPR/B-Experimente eigentlich so gewählt ist, dass mögliche Korrelationen minimiert werden: Erstens werden die Messeinstellungen zufällig und unabhängig voneinander gewählt. Zweitens werden die Geräte räumlich so angeordnet und der zeitliche Ablauf so arrangiert, dass sich viele der Ereignisse in den Experimenten nach normalen Standards nicht beeinflussen können. Im Besonderen werden die Geräte so angeordnet, dass sie raumartig zueinander liegen, das heißt, dass sie nur mit Wirkungen schneller als Lichtgeschwindigkeiten verbunden werden können. Da die Spezielle Relativitätstheorie solche Wirkungen jedoch verbietet, scheint eine gegenseitige Einflussnahme der beiden Geräte ausgeschlossen.
Man kann dies gut an den folgenden Raumzeit-Diagrammen illustrieren:
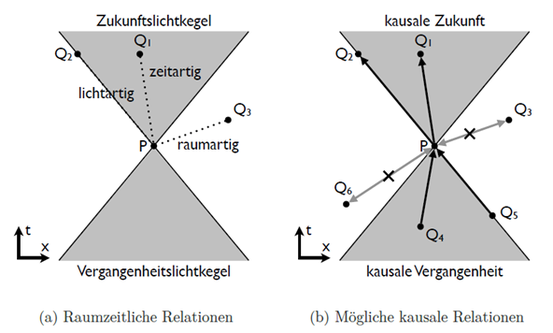
Die graue Fläche bilden jeweils den Lichtkegel eines Ereignisses P ab. Die Punkte Q1, Q2, Q3, etc. stehen für weitere Ereignisse in Raum und Zeit. P und ein gegebenes Ereignis Q können nun auf drei Weisen raumzeitlich zueinander liegen:
zeitartig: Wenn ein gegebenes Ereignis Q innerhalb des Lichtkegels von P liegt, dann liegt Q zeitartig zu P. In dem Fall kann P mit Q durch einen (kausalen) Prozess verbunden werden, der sich mit Unterlichtgeschwindigkeit ausbreitet.
lichtartig: Wenn ein gegebenes Ereignis Q auf dem Lichtkegel von P liegt, dann liegt Q lichtartig zu P. In dem Fall kann P mit Q durch einen (kausalen) Prozess verbunden werden, der sich mit Lichtgeschwindigkeit ausbreitet.
raumartig: Wenn ein gegebenes Ereignis Q außerhalb des Lichtkegels von P liegt, dann liegt Q raumartig zu P. In dem Fall kann P mit Q nur durch einen (kausalen) Prozess verbunden werden, der sich mit Überlichtgeschwindigkeit ausbreitet.
Die Ereignisse innerhalb (Q1) und auf (Q2) dem Lichtkegel von P liegen lokal zu P. Die Ereignisse außerhalb (Q3) dem Lichtkegel von P liegen hingegen nicht-lokal zu P. Gemäß der Standardinterpretation der Relativitätstheorie können sich nur Ereignisse (kausal) beeinflussen, die lokal zueinander liegen. Das heißt es gilt:
Das (kausale) Einstein-Lokalitätsprinzip (ELP): Es gibt keine (kausalen) Prozesse schneller als Licht.
Die Relativitätstheorie ist in dem Sinne eine lokale Theorie, dass gemäß ihrer Standardinterpretation nur lokale Prozesse physikalisch möglich sind. Wenn (ELP) wahr ist, dann können raumartig getrennte Ereignisse einander nicht (kausal) beeinflussen. Dann kann P in Grafik 2 nur von Ereignissen verursacht werden, die auf oder innerhalb seines Vergangenheitslichtkegels liegen. Und dann kann P nur Ereignisse verursachen, die auf oder innerhalb seines Zukunftslichtkegels liegen.
Die spezifische Situation in den EPR/B-Experimenten lässt sich nun ebenfalls in einem Raumzeit-Diagramm illustrieren:
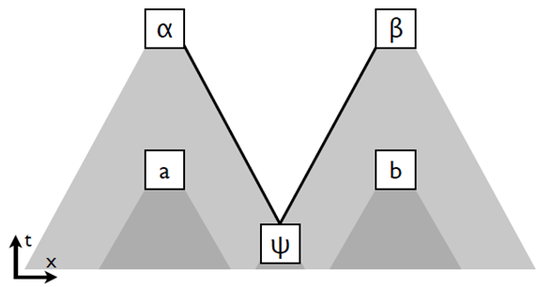
Die beiden Punkte α und β bilden die zwei Messereignisse α und β und Ψ bildet das Emissionsereignis ab. Die hellkrauen Flächen stehen für die Vergangenheitslichtkegel von α und β. Die weiße Fläche zwischen diesen grauen Flächen ist der Zukunftslichtkegel vom Messereignis Ψ. Die schwarze Linie zwischen Ψ und α bzw. Ψ und β repräsentieren den Weg der Photonen von der Emissionsquelle zu den Messgeräten. Die Grafik 3 macht klar, dass wenn (ELP) wahr ist, die Messereignisse α und β nur von den Ereignissen in ihren Vergangenheitslichtkegeln kausal beeinflusst werden können. Im Besonderen können die Messereignisse sich nicht gegenseitig oder von den Einstellungsereignisse a und b am anderen Gerät kausal beeinflusst werden. Darüber hinaus kann das Emissionsereignis Ψ trivialerweise nur α und β und nicht a und b kausal beeinflussen, da es in der Emission von Lichtquanten besteht.
Die verbleibenden möglichen Einflüsse zwischen Ereignissen in EPR/B-Experimenten ist in Grafik 4 dargestellt. Die Pfeile zwischen den Variablen (Erei-gnissen) heißen "kausale Graphen" und repräsentieren eine kausale Struktur:
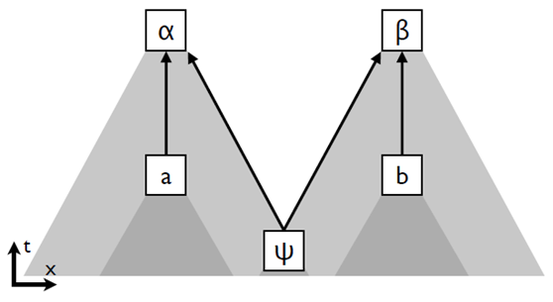
Die möglichen kausalen Einflüsse in EPR/B-Experimenten sind nach (ELP) also stark beschränkt. Trotzdem gibt es in EPR/B-Experimenten diese starken Korrelationen zwischen den Messereignissen α und β. Und im nächsten Abschnitt werden wir sehen, dass diese zu stark sind, um im Rahmen von (ELP) erklärt zu werden. Mit anderen Worten: α und β scheinen sich auf eine nicht-lokale Weise zu beeinflussen und (ELP) scheint in Folge in der Quantenwelt nicht zu gelten.
3.2. Bells Version
John S. Bell legte in seinem Aufsatz von 1964 ein EPR/B-Experiment wie in Grafik 4 zugrunde. Das Messergebnis A(α) von α kann "Spin-Up" in Richtung a mit dem Messwert +1 oder "Spin-Down" in Richtung a mit dem Messwert - 1 betragen. Das Messergebnis B(β) von β kann "Spin-Up" in Richtung b mit dem Messwert +1 oder "Spin-Down" in Richtung a mit dem Messwert -1 betragen.
Die Messergebnisse A(α) und B(β) sind stark korreliert. Außerdem wurden die Korrelationen im Anschluss an die EPR/B-Experimente von Alain Aspect unzählige Male bestätigt. Das alles schließt einen Zufall aus. John Bell geht deshalb davon aus, dass die Messergebnisse A(α) und B(β) durch die Messrichtungen a und b und einen verborgenen Parameter λ beeinflusst werden. Sprich: A(a, λ) = ± 1 und B(b, λ) = ± 1. Der Erwartungswert des Produktes der Messungen ist dann:
A(a, λ)B(b, λ)
Dieser Erwartungswert E(a, b) gilt unter den angegebenen Voraussetzungen:
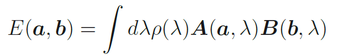
Die Formel 1 ist eine Lokalitätsannahme. Heutzutage wird sie als Bedingung der lokalen Faktorisierbarkeit bezeichnet. Diese Lokalitätsannahme ist vor allem mit dem Prinzip (ELP) aus der Relativitätstheorie motiviert. Zudem kann man aus dem Erwartungswert E(a, b) ablesen, ob A(α) und B(β) korreliert sind.
Bell unterscheidet zwischen drei Richtungen u, v und w, in denen an die Messgeräte A und B die jeweilige Spinwerte messen können und leitet daraus die folgende Ungleichung ab. Sie ist heute als die Bellsche Ungleichung bekannt:
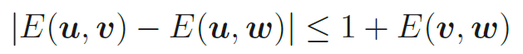
Der entscheidende Schritt im Bellschen Beweis besteht darin, dass John Bell zeigt, dass der mathematischen Beschreibung der Quantentheorie von EPR/B-Experimenten die Bellsche Ungleichung verletzt. Denn es gilt für den Erwartungswert A(a, λ)B(b, λ) nach der Quantentheorie Folgendes:
EQM(a,b) = -ab.
Dabei ist ab das Skalarprodukt der Messrichtungen, das durch cos(φ), also durch den Winkel φ zwischen den beiden Richtungen bestimmt wird. Wird z.B. an beiden Messgeräten in der gleichen Richtung gemessen, ist der Erwartungswert EQM(a, a) gleich −1, d.h. auf einer Seite findet man "Spin-down " und auf der anderen Seite "Spin-up". Wählt man nun die Richtungen wie nachstehend:
u = (v - w) / |v - w| und v senkrecht auf w (d.h. vw = 0).
Dann ergibt der Erwartungswert nach Einsetzen in Formel 2 einen Widerspruch:
√2 ≤ 1.
Der Bellsche Beweis besagt somit Folgendes: Jede Theorie, welche nicht die Erwartungswerte der in der Formel 1 ausgedrückten Lokalitätsannahme und damit die in der Formel 2 ausgedrückten Bellschen Ungleichung erfüllt, kann auch nicht die Erwartungswerte - und damit die EPR-Korrelationen - vorhersagen und erklären, die aus der Quantenmechanik folgen. Damit stehen diese lokalen Theorien aber in Konflikt mit der Empirie. Denn die Erwartungswerte der Quantenmechanik und damit die EPR-Korrelationen sind experimentell bestätigt.
3.3. moderne Version
Die Diskussion in den letzten sechzig Jahren hat gezeigt, dass das Ergebnis von Bells Beweis auch aus einem schwächeren Satz von Annahmen abgeleitet werden kann. Im folgenden soll eine moderne Rekonstruktion von Bells Beweis skizziert werden. Außerdem werden die impliziten inhaltlichen und methodischen Annahme und Folgen aus dem Beweis explizit gemacht. Der Bellsche Beweis ist ein mathematisches Argument, das in seiner stärksten Version mit bedingten Wahrscheinlichkeiten formuliert wird. Die mathematische Präzision des Beweises ist einerseits eine seiner Stärken, andererseits ist die mathematische Form des Beweises auch eine Schwäche, da nicht eindeutig ist, wie die mathematischen Formeln metaphysisch zu interpretieren sind. Das heißt, es besteht ein Dissens in der Fachwelt darüber, was der Bellsche Beweis über die Quantenwelt aussagt.
Der Bellsche Beweis nimmt seinen Ausgangspunkt bei EPR-Korrelationen. Das sind bei gleichen Messeinstellungen perfekte Korrelationen zwischen raumartig zueinander liegenden Messereignissen und bei verdrehten Messeinstellungen entsprechend schwächere. Es handelt sich um eine der zentralen Prämissen wissenschaftlichen Arbeitens, dass Korrelationen erklärungsbedürftig sind. Besonders starke und stabile Korrelationen wie die EPR-Korrelationen werden in der Regel über kausale Relationen erklärt. Gemäß der Standardinterpretation der Relativitätstheorie gilt ein Prinzip (ELP), nach dem diese EPR-Korrelationen nur durch lokale Prozesse erklärt werden können. John Bell wollte dieser Möglichkeit Raum geben und nahm an, dass der Zustand der Photonen an der Quelle C neben dem quantenmechanischen Zustandsbeschreibung durch Ψ auch noch durch eine im gegenwärtigen mathematischen Formalismus der Quantenmechanik verborgene Variable λ beschrieben werden kann. Diese Variable kann prinzipiell lokal sein in dem Sinne, dass sie eine lokale Informationsübertragung zwischen den Photonen am Emissionsort beschreibt. In dem Fall könnten die EPR-Korrelationen lokal durch λ erklärt werden. Halten wir dies in einer Grafik fest:
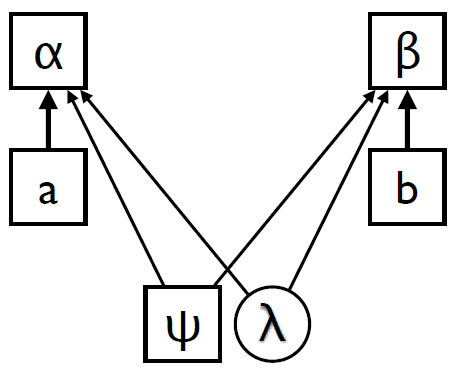
Der Bellsche Beweis kann nun als ein mathematisches Argument betrachtet werden. Es besagt in der Kurzform, dass keine Theorie mit lokalen verborgenen Variablen die EPR-Korrelationen erklären kann. Etwas ausführlicher hat es die logische Form einer reductio ad absurdum. Es geht von drei Annahmen aus:
(A1) keine Rückwärtsverursachung: kausale Relationen (Prozesse) sind zeitlich immer vorwärts gerichtet.
(A2) keine zusätzlichen Interventionen: der Quantenzustand Ψ und a und b sind keine kausalen Ursachen der Messereignisse α und β.
(A3) kausale Markov-Bedingung: Gegeben ihre direkten Ursachen Z wird eine Variable X statistisch unabhängig von allen Variablen Y, die keine Wirkungen von ihr sind: P(X|Y Z) = P(X|Z).
Die drei Hintergrundannahmen (A1), (A2) und (A3) sind sehr plausibel. Jedoch ist die Diskussion um die Erklärung der EPR-Korrelationen so knifflig, dass selbst diese Annahmen bezweifelt werden. Bells zeigt nun auf, dass die Annahme einer lokalen verborgenen Variable im mathematischen Formalismus der Quantenmechanik plus die Annahmen (A1) - (A3) die Ableitung bestimmter statistischer Konsequenzen erlaubt. Diese Konsequenzen drücken sich in der Bellschen Ungleichung aus, welche in Formel 2 niedergeschrieben ist und eine obere Grenze für die Stärke von Korrelationen aus lokalen Strukturen angibt.
Die entscheidende Schluss besteht nun darin, dass Bell zeigt, dass diese Konsequenzen in Widerspruch zu den gemessenen Statistiken stehen. Das heißt die experimentell nachgewiesenen Korrelationen sind stärker als es die Bellsche Ungleichung erlaubt. Diesen Schluss kann nachvollzogen werden, wenn man mithilfe von (A3) aus den Graphen folgende statistische Tatsachen ableitet:
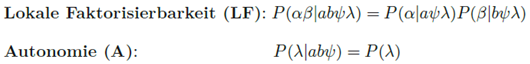
Die Faktorisierbarkeitsbedingung formalisiert die Tatsache, dass in der gegebenen Struktur jedes der Messergebnisse direkt nur von seiner je lokalen Messeinstellung, vom Quantenzustand und den verborgenen Parametern beeinflusst wird, nicht aber vom anderen Messergebnis oder der entfernten Messeinstellung. Die Autonomiebedingung hingegen resultiert aus der Tatsache, dass es keine Einflüsse zwischen der Variablen λ einerseits und den Messeinstellungen und dem Quantenzustand ψ andererseits gibt.
Diese beiden probabilistischen Bedingungen sind das mathematische Fundament von Bells Beweis, aus denen er seine Ungleichung ableitet. Die experimentelle Verletzung dieser Ungleichung zeigt die Falschheit bestimmter Annahmen. Bei den Annahmen können wir nun zwei Ebenen unterscheiden: Erstens muss mindestens eine der probabilistischen Annahmen lokale Faktorisierbarkeit oder Autonomie falsch sein. Zweitens muss mindestens eine der kausalen Annahmen das Prinzip der kausalen Einstein-Lokalität (ELP) oder einer der Hinter-grundannahmen (A1) - (A3) falsch sein. Das Argument lautet dann wie folgt:
P1. Die kausale Einstein-Lokalität (ELP) und die Hintergrundannahmen (A1), (A2) und (A3) implizieren die zwei probabilistischen Annahmen (LF) und
(A).
(ELP) ∧
(A1) ∧ (A2) ∧ (A3) → (LF) ∧ (A).
P2. Die probabilistischen
Annahmen lokale Faktorisierbarkeit (BU) und Autonomie (A) implizieren die Bellsche Ungleichung (BU).
(LF) ∧ (A) → (BU).
P3. Die Bellsche Ungleichung ist experimentell verletzt.
¬(BU).
K1. Also:
Die probabilistische Annahme lokale Faktorisierbarkeit (BU) oder Autonomie (A) ist falsch. (folgt aus P2. und P3 qua modus tollens).
¬(A)∨¬(LF).
K2. Also: Die Hintergrundannahme (ELP), (A1), (A2) oder (A3) ist falsch. (folgt aus P1. und C1 qua modus tollens).
¬(ELP)∨¬(HA).
Diese explizite Struktur des Argumentes verdeutlicht noch einmal, dass es einen mathematischen Kern des Argumentes gibt, nämlich den Schluss von P2. und P3. auf K1. Dieser Kern des Argumentes ist weitestgehend unstrittig. Die Prämisse P1., welche den Schluss auf K2. ermöglicht, hat eher den Status einer interpretierenden Prämisse, welche dem formalen Argument eine kausale Deutung verleiht. Es ist erst dieser kausale Interpretationsrahmen, der dem formalen Argument seine weitreichende naturphilosophische Bedeutung verleiht.
4. Fazit
Das Bellsche Argument zeigt also, dass jeweils mindestens eine der probabilistischen Annahmen und eine der kausalen Annahmen falsch sein muss:
probabilistische Annahmen: Lokale Faktorisierbarkeit (LF), Autonomie (A).
kausale Annahmen: kausales Einstein-Lokalitätsprinzip (ELP), keine Rückwärtsverursachung (A1), keine zusätzliche Intervention (A2), kausale Markov-Bedingung (A3).
Das Bellsche Argument ist damit ein typisches No-Go-Theorem. Das heißt es beweist, dass es physikalisch (empirisch) nicht möglich ist, dass alle probabilistischen Annahmen oder dass alle kausalen Annahmen wahr sind. Das Besondere an diesem Argument ist, dass die Annahmen sowohl für Laien als auch für Fachleute sehr plausibel sind. Das Argument zeigt also, dass die Quantenwelt radikal mit unseren alltäglichen und klassisch-physikalischen Annahmen bricht.
Es scheint fast unmöglich zu sein, auf rein probabilistischer Ebene ein philosophisch überzeugendes Argument dafür zu finden, welche der probabilistischen Annahmen plausiblerweise falsch ist. Praktisch alle Autoren konzentrieren sich deshalb auf die kausalen Annahmen. Darüber hinaus interpretieren die meisten Autoren die Verletzung der Ungleichung als ein Zeichen für die Nicht-Gültigkeit des kausalen Einstein-Lokalitätsprinzips (ELP) in der Quantenwelt. Das hat bei Lichte betrachtet wohl auch damit zu tun, dass zwei der populärsten Interpretationen der Quantentheorie - die Ghirardi–Rimini–Weber-Theorie und die De-Broglie-Bohm-Theorie - dezidiert nicht-lokale Theorien sind.

zusammengefasste Literatur
Dieser Text basiert auf einer Zusammenfassung der Arbeiten von Paul Näger zu diesem Thema. Bald erscheint seine Dissertation zum Thema als
Buch:
Näger, Paul M. (forthcoming). Quantum Entanglement and Causation. Boston Studies in the Philosophy of Science. Cham: Springer.
Siehe auch
Albert Einstein über die Quantentheorie
Hans Reichenbach über Kausalität
Holismus in der Quantenmechanik
Mathematische Grundlagen der Quantenmechanik
Ontischer Strukturenrealismus
Outcome Dependence versus Parameter Dependence
Rückwärtsverursachung
Scholarpedia
(Travis Norsen, Sheldon Goldstein et. al)
Stanford Encyclopedia of Philosophy (Wayne Myrvold, Marco Genovese)
What Bell Did (Tim Maudlin)
 Philoclopedia
Philoclopedia
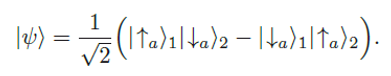
Kommentar schreiben
WissensWert (Donnerstag, 10 Mai 2018 14:27)
heute auf Spektrum erschienen: https://www.spektrum.de/news/computerspieler-widerlegen-einstein/1564842
Philoclopedia (Samstag, 05 Oktober 2019 21:07)
https://www.uni-muenchen.de/forschung/news/2017/weinfurter_bellscheungleichung.html