Ein Kontrafaktisches Konditional hat die folgende Form:

KK. Wenn A der Fall wäre, dann wäre B der Fall.

Formal:

KK_For. A □® B.

Ein Konditional hat ganz allgemein die Form "Wenn A, dann B."

Dabei ist A das Antezedens und B das Konsequens. Das "Konditional zeigt an, dass wenn das Antezedens wahr ist, dann ist auch das Konsequenz wahr.

Nach Ernest Adams werden 2 Arten von Konditionalen unterschieden:[1]

1. Wenn A nicht der Fall ist, dann ist B der Fall.
2. Wenn A nicht der Fall wäre, dann wäre B der Fall.

Ein klassisches Beispiel:

1. Wenn Oswald Kennedy nicht erschossen hat, dann hat es jemand anderes getan.
2. Wenn Oswald Kennedy nicht erschossen hätte, dann hätte es jemand anderes getan.

Konditionale der Art 1. werden indikativische Konditionale genannt. Denn bei ihm ist das Antezedenz möglicherweise wahr. Das heißt, es kann der Fall oder nicht der Fall sein, dass Oswald Kennedy erschossen hat. Durch den indikativen Modus wird angezeigt, dass die Erschießung Kennedys als faktisches  Ereignis feststeht. Also hat entweder Oswald oder jemand anderes Kennedy erschossen und das indikativische Konditional 1. ist auf jeden Fall wahr.

Konditionale der Art 2. werden kontrafaktische Konditionale genannt. Denn bei ihm ist das Antezedenz tatsächlich falsch. Das heißt, es ist tatsächlich der Fall, dass Oswald Kennedy erschossen hat. Es wird eine kontrafaktische Annahme darüber getroffen, dass jemand anderes Kennedy erschossen hätte, wenn Oswald es nicht getan hätte. Also ist das KK 2. dann wahr, wenn jemand anderes Kennedy erschossen hätte, wenn es nicht Oswald getan hätte.

Kontrafaktische Konditionale spielen in alltäglichen, wissenschaftlichen und philosophischen Begründungszusammenhängen eine herausragende Rolle.

Auch Handlungen können durch sie erklärt oder gerechtfertigt werden:

a. Handlung: Wenn ich es dir erzählt hätte, wäre es keine Überraschung gewesen.

Ferner lassen sich so notwendige und kausale Zusammenhänge ausdrücken:

b. notwendiger Zusammenhang: Wenn es ein Rubin wäre, dann wäre der Stein rot.

c. kausaler Zusammenhang: Wenn der Ball die Scheibe getroffen hätte, wäre die Scheibe zersprungen.

In der Metaphysik, Naturphilosophie und Wissenschaftstheorie dienen KK insbesondere als Rekonstruktionsmittel für die Analyse von zentralen Begriffen:

d. Disposition: X hat die Disposition "zerbrechlich sein", gdw. gilt: Wenn man X auf den harten Boden fallen gelassen hätte, dann wäre X zerbrochen.

e. Kausalität: A ist die Ursache der Wirkung B, gdw. gilt: Wenn das Ereignis A nicht eingetreten wäre, dann wäre auch das Ereignis B nicht eingetreten.

f. Handlungsfreiheit: Die Handlung H der Person P ist frei, gdw. gilt:

Wenn P sich anders entschieden hätte, dann hätte P anders gehandelt.

g. Naturgesetz: G ist ein Naturgesetz, nur dann wenn für eine große Klasse von Ereignissen E gilt: Selbst wenn E eingetreten wären, wäre G wahr.

Einerseits sind KK bei der Analyse von weiteren Begriffen äußerst hilfreich. Andererseits bereitet ihre Analyse selbst jedoch große Schwierigkeiten.

Fangen wir also wieder ganz einfach mit dem einfachen Konditional "Wenn A, dann B" an. Formal ist die Bedeutung eines solches Konditionals nichts mehr als die Verbindung der Bedeutungen der Aussagen durch ein Konnektiv.

Die einfachste Formalisierung dieser Verbindung ist in der klassischen, extensionalen Logik die materiale Implikaiton (A → B). Die Bedeutung eines komplexen Satzes wird als Wahrheitsfunktion der Wahrheitswerte seiner Teilsätze aufgefast. Und die Wahrheitsbedingung von "A → B" sind folglich durch die Verteilungen der Wahrheitswerte "wahr" und "falsch" gegeben. A → B ist also falsch, gdw. A wahr und B falsch ist. In allen anderen Fällen ist der Satz wahr.

Das kontrafaktische Konditional kann aber formal nicht als materiale Implikation expliziert werden. Denn unter der materialen Implikation sind alle Konditionale mit falschem Antezdenz immer wahr. Da kontrafaktische Konditionale aber qua definitonem ein falches Antezedenz besitzen, müssten unter der materialen Implikation alle Kontrafaktischen Konditionale wahr sein.

Es ist aber ein wesentliches Merkmal von Kontrafaktischen Konditonalen, dass einige von ihnen wahr sind, andere hingegen aber nicht. Betrachten wir etwa:

(i) Wenn die Vase auf den Boden gefallen wäre, wäre sie zersprungen.

(ii) Wenn die Vase auf den Boden gefallen wäre, wäre sie verschwunden.

Das erste Kontrafaktische Konditional ist offensichtlich wahr, das zweite nicht.

Eine anspruchsvollere Formalisierung der Konditionalverbindung ist in der intensionalen Modallogik die strikte Implikation (□ (A → C)). Die ist wahr, genau dann wenn sie notwendig, d.h. in allen möglichen Welten wahr ist.

Allerdings zeigt (iii), dass sich kontrafaktische Konditionale auch nicht als strikte Implikationen formalisieren lassen:

(iii) Wenn weniger Menschen rauchen würden, wären viele von ihnen gesünder.

Als kontrafaktisches Konditional ist (iii) wahr. Interpretiert als strikte Implikation ist (iii) falsch. Denn es gibt sicher mögliche Welten, in denen sie nicht wahr ist.

Die Wahrheitsbedingungen bzw. Semantik kontrafaktischer Konditionale lässt sich also weder auf die materiale noch auf die strikte Implikation reduzieren.

Vor diesem Hintergrund hat Nelson Goodman den ersten Meilenstein bei der Analyse kontrafaktischer Konditionale gelegt. Goodman legt den Fokus nicht so sehr auf die tatsächliche Wahrheit der Teilsätze oder auf die notwendige Wahrheit des komplexen Satzes. Vielmehr besagt Nelson Goodmans Ansatz im Kern:

Metalinguistische Analyse: Ein kontrafaktisches Konditional KK ist wahr, gdw. es ein deduktives Argument zum Konsequens B von KK gibt, welches das Antezedens A und bestimmte, tatsächlich wahre Prämissen C enthält.

Beispiel 1:

(iv) Wenn dieses Elektron sich in das magnetische Feld bewegen würde, dann würde es einer gekrümmten Bahn folgen.

Nach der metalinguistischen Analyse ist das kontrafaktische Konditonal (iv) wahr.

Denn: Es gibt ein entsprechendes deduktives Argument für sein Konsequenz:

P1. Dieses Elektron bewegt sich in das magnetische Feld (Antezedenz).

P2. Alle Elektronen haben eine negative Ladung (wahre Prämisse I).

P3. Alle negativ geladenen Teilchen bewegen sich in einem magnetischen Feld in einer gekrümmten Bahn (wahre Prämisse II).
K1. Also: Dieses Elektron folgt einer gekrümmten Bahn (Konsequenz).

Ein solches Argument muss nach Godman nun folgenden Bedingungen genügen:

1. Logische Kompatibilität: Die tatsächlich wahren Prämissen dürfen nicht die Negation des Antezedenz, welche ebenfalls eine tatsächliche Wahrheit ist, enthalten. Denn ansonsten würden sich die wahren Prämissen und das falsche Antezedenz widersprechen und aus widersprüchlichen Prämissen folgt Beliebiges.

Also: Die tatsächliche Wahrheit der Prämissen P2. und P3. impliziert nicht, dass dieses Elektron sich nicht in das magnetische Feld bewegt. Bedingung 1 ist erfüllt.

2. Naturgesetze: Die tatsächlich wahren Prämissen müssen die geltenden Naturgesetze enthalten und somit als inferentielle Brückenprinzipien den Übergang vom Antezedenz zum Konsequenz ermöglichen.

Also: Die tatsächlich wahren Prämissen P2., P3. enthalten die relevanten Natur-gesetze und ermöglichen den Übergang von P1. zu K1. Bedingung 2 ist erfüllt.

Goodmans metalinguistische Analyse sowie die beiden Bedingungen sind nicht hinreichend, um die Wahrheitsbedingungen von KK zu explizieren.

Denn es fehlt noch eine dritte Bedingung:

3. Unabhängigkeit: Wenn das tatsächlich falsche Antezedenz wahr wäre, dann wären deshalb nicht die tatsächlich wahren Prämissen falsch.

Diese notwendige Bedingung ist aber ebenfalls ein kontrafaktisches Konditional.

Also setzt Goodmans Analyse der Wahrheit eines kontrafaktischen Konditionals bereits die Wahrheit eines kontrafaktischen Konditionals voraus und endet damit in einem infiniten Regress. Goodman betrachtete dieses Problem als unlösbar.

Ungefähr 20 Jahre nach Goodman entwerfen Robert Stalnaker und in Anschluss an ihn David Lewis eine gänzlich neue Analyse kontrafaktischer Konditionale. 

Dabei formalisieren sowohl Stalnaker als auch Lewis das kontrafaktische Konditional durch das primitive Konditionalkonnektiv □→ und interpretieren dieses im Rahmen einer je eigenen, kompositionalen Möglichen-Welten-Semantik.

Robert Stalnaker analysiert die Wahrheitsbedingung so: Ein kontrafaktisches Konditional A □→ B ist wahr in der (aktualen) Welt w, gdw. das Konsequenz B wahr ist in der Welt w*, die der Wert der Selektionsfunktion f(A, w) ist.

Und die Bedeutung eines kontrafaktischen Konditionals analysiert er so: A repräsentiert die Menge von Welten, in denen das Antezedenz A wahr ist.

Dabei wählt die Selektionsfunktion f(A, w) die Welt w* aus, in der A wahr ist und die w, so weit als es die Wahrheit von A erlaubt, maximal ähnlich ist.

Die Schwachstelle von Stalnakers (und Lewis) Analyse ist die Frage, wie oder worin die (maximale) Ähnlichkeitsrelation zwischen w und w* besteht. Für Stalnaker ergibt sich die Antwort auf diese Frage pragmatisch aus dem Kontext.

Jede Ähnlichkeitsrelation R muss aber u.a. diesen Bedingungen genügen:

·        Die Relation R ist transitiv (wenn aRb und bRc, dann auch aRc)

·        Die Relation R ist antisymmetrisch (wenn aRb und bRa, dann a = b)

·        Die Relation R ist reflexiv (aRa) und

·        Die Relation R ist total (jedes Element ist mit jedem anderen vergleichbar).

Dies ergibt eine lineare Ordnung der möglichen Welten, in der es immer genau eine Welt w* gibt, die der aktualen Welt w am ähnlichsten ist.

Diese lineare Ordnung schlägt sich auch in Stalnakers Konditionallogik nieder. Stalnaker setzt den Satz vom ausgeschlossenen Dritten axiomatisch voraus.

David Lewis übernimmt viele von Stalnakers Kerngedanken. Den Satz vom ausgeschlossenen Dritten und die Antisymmetriebedingung lässt er aber fallen.

Daraus folgt, dass nach Lewis auch zwei oder mehr Welten w*,  w**, usw. der aktualen maximal ähnlich (bzw. minimal unähnlich) sein können.

Lewis entwickelt ein Sphärenmodell, in dem die Ähnlichkeitsrelation und die Ordnung der möglichen Welten explizit repräsentiert ist. Umso ähnlicher eine Welt der aktualen Welt ist, desto näher ist sie dieser im Sphärenmodell. Und wenn zwei Welten w* und w** w gleichähnlich sind, gehören sie derselben Sphäre an.

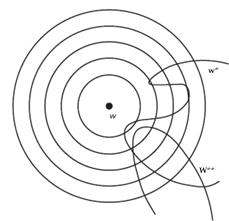
David Lewis analysiert die Wahrheitsbedingung jetzt so: Ein kontrafaktisches Konditional A □→ B ist wahr in der (aktualen) Welt w, gdw. es mindestens eine A ∧ B-Welt w* gibt, die w ähnlicher ist als alle A ∧ ¬B-Welten w´.

Beispiel: Das kontrafaktische Konditional "Wenn der Ball die Scheibe getroffen hätte, wäre die Scheibe zersprungen" ist wahr in der (aktualen) Welt w, gdw. es mindestens eine mögliche Welt w* gibt, in der der Ball die Scheibe getroffen hat und die Scheibe zersprungen ist und wenn diese mögliche Welt w* der aktualen Welt w ähnlicher ist als alle möglichen Welten, in denen der Ball die Scheibe getroffen hat und die Scheibe nicht zersprungen ist.

Das trifft die Bedeutung kontrafaktischer Konditionale nach der Meinung vieler Philosophen sehr genau! Außerdem führt die Stalnaker-Lewis Analyse nicht mehr in einen Regress. Denn sie gründet nicht mehr auf einem anderen kontrafaktischen Konditional, sondern auf der zentralen Ähnlichkeitsrelation.

Stalnaker macht geltend, dass diese Ähnlichkeitsrelation pragmatisch festgelegt werden muss. Lewis möchte die Ähnlichkeitsrelation durch sein Sphärenmodell erfassen. Beide bleiben uns die Frage schuldig, wie man mögliche Welten auf ihre Ähnlichkeit vergleichen soll und kann und welche Eigenschaften der möglichen Welten hierfür herangezogen werden sollen. Einig sind sie sich darin, dass dies keine modalen (etwa kontrafaktischen) Eigenschaften sein dürfen.

Kit Fine erläutert ein Problem der Ähnlichkeitsrelation am Nixon-Beispiel:

(v) Wenn Nixon den roten Knopf gedrückt hätte, hätte es einen nuklearen Holocaust gegeben.

Das kontrafaktische Konditional (v) ist (intuitiv) wahr. Dahingegen weißt die Ähnlichkeitsrelation (v) aber als falsch aus. Denn in Anbetracht der Entwicklung der aktualen Welt nach Nixon sind mögliche Welten, in denen es eine Fehlzündung und keinen nuklearen Holocaust gab unserer aktualen Welt ähnlicher als eine Welt, in der es zum nuklearen Holocaust kam und deren Verlauf somit extrem von der aktualen Welt abweicht. Allgemein ging es Fine um Fälle, in denen das Antezedenz zu einer enormen Abweichung im Weltverlauf führt.

David Lewis antwortete daraus mit der Formulierung hierarchischer Prinzipien:

hierarchische Prinzipien: Die Welt w* ist der aktualen Welt w am ähnlichsten, gdw. (a) w* im Großen und Ganzen mit den Fakten der aktualen Welt übereinstimmt, d.h. dass w* und w, soweit es die anderen Prinzipien zulassen, identisch sind. (b) w* den gleichen Naturgesetzen unterliegt und es von diesen nur eine minimale Abweichung gibt, d.h. eben nur die Abweichung, die notwendig ist, um das Antezedenz wahr zu machen.

Dabei gilt: Im Zweifelsfall ist Prinzip (b) höher zu gewichten als Prinzip (a).

Eine Konsequenz aus diesen beiden Prinzipien ist, dass w* bis kurz vor der Antezedenszeit (a) einen identischen Weltverlauf haben und (b) denselben Naturgesetzen unterliegen muss. Bei der Antezedenzzeit ändert eine punktuelle Abweichung von den Naturgesetzen den Verlauf von w* und macht das Antezedenz wahr. Und nach der Antezedenzeit entwickelt sich w* in größtmöglicher Übereinstimmung mit dem Verlauf und den Naturgesetzen in w.

Mit den hierarchischen Prinzipien wird (v) als wahr und damit korrekt evaluiert. Allerdings haben eine Reihe von strukturell ähnlichen Gegenbeispielen gezeigt, dass nicht nur allgemeine Weltverläufe und Naturgesetze, sondern auch singuläre Fakten relevant für die Analyse kontrafaktischer Konditionale sind.

Pavel Tichy hat ein solches Gegenbeispiel entworfen:

(vi) Wenn gutes Wetter herrschen würde, würde Hubert einen Hut tragen.

I: Nehmen wir an, dass Hubert bei schlechtem Wetter immer einen Hut trägt. Dass bei gutem Wetter die Chancen 50 zu 50 stehen, dass Hubert einen Hut trägt. Und dass es regnet und Hubert entsprechend einen Hut trägt.

Unter den Annahmen I ist das kontrafaktische Konditional (vi) intuitiv nicht klarerweise wahr. Denn wenn gutes Wetter herrschen würde, würden die Chancen 50 zu 50 stehen, dass Hubert einen Hut tragen würde. Lewis ursprüngliche Analyse kontrafaktischer Konditionale weißt (vi) aber als wahr aus und fängt damit nicht unsere Intuition ein. Denn der Weltverlauf einer Welt w*, in der gutes Wetter herrscht und Hubert einen Hut trägt, ist der aktualen Welt w, in der es regnet und Hubert einen Hut trägt ähnlicher als eine Welt w**, in der gutes Wetter herrscht und Hubert keinen Hut trägt. Lewis revidierte Analyse mit den hierarchischen Prinzipien fängt unsere Intuition hingegen ein. Denn partikulare Fakten spielen in der revidierten Analyse keine Rolle mehr.

II: Nehmen wir an, dass Hubert Exzentriker ist und nach den folgenden Regeln  entscheidet, ob er beim Verlassen des Hauses inen Hut aufsetzt: (1) Hubert wirft jeden Morgen eine Münze und schaut erst dann aus dem Fenster. (2) Wenn schönes Wetter ist und die Münze "Zahl" zeigt, trägt Hubert keinen Hut. (3)  Wenn schönes Wetter ist und die Münze "Kopf" zeigt, trägt Hubert einen Hut. (4)  Wenn schlechtes Wetter ist, trägt Hubert unabhängig vom Münzwurf einen Hut. (5) Und in der aktualen Welt ist schlechtes Wetter, die Münze zeigt "Kopf" und Hubert trägt dementsprechend einen Hut. 

Unter den Annahmen II ist das kontrafaktische Konditional (vi) intuitiv wahr. Denn wenn gutes Wetter herrschen würde, würde Hubert gemäß (3) trotzdem einen Hut tragen, da die Münze "Kopf" zeigt. Lewis kann den Umstand in seiner revidierten Analyse aber nicht mehr erfassen, da die partikulare Tatsache, dass die Münze in der aktualen Welt "Kopf" zeigt, keine Rolle mehr spielt.

Ein kontrafaktisches Konditional wie (vi) kann also nur dann korrekt analysiert werden, wenn einerseits die Fakten aufgegeben werden, die von der Negation des Antezedenz abhängen. Und wenn andererseits möglichst viele vom Antezedenz unabhängige Fakten beibehalten werden werden. Das heißt eine angemessene Analyse muss die tatsächliche Abhängigkeit von partikularen Fakten und der Wahrheit des kontrafaktischen Konditionale angeben können.

Lewis Analyse leistet dies nicht, da sie kontrafaktische Konditionale zur Explikation von Abhängigkeit verwendet. Das Finden eines geeigneten Abhängig-keitsbegriffes ist daher Hauptgegenstand der aktuellen Diskussion und Forschung über kontrafaktische Konditionale und ihre Wahrheitsbedingungen.

Die kontrafaktische Theorie der Kausalität

Stanford Encyclopedia of Philosophy

zum vorherigen Blogeintrag                                        zum nächsten Blogeintrag 

Liste aller Blogbeiträge zum Thema "Logik"