Die Pessimistische Metainduktion (PMI) ist ein auf den Aufsatz "A Confutation of Convergent Realism" von Larry Laudan[] zurückgehendes Argument gegen den wissenschaftlichen Realismus. Es kann so rekonstruiert werden:

P1. Es gab in der Vergangenheit viele wissenschaftliche Theorien Tv, die empirisch erfolgreich waren.

P2. Die meisten dieser Theorien Tv wurden inzwischen zurückgewiesen. Nach heutigem Kenntnisstand sind sie nicht wahr und ihre theoretischen Terme referieren nicht auf theoretische Entitäten.

P3. Die gegenwärtigen (erfolgreichen) wissenschaftlichen Theorien T_G sind nicht von völlig anderer Art wie die Theorien T_V (gleiche Methoden, etc.).

C1. Also: Wir haben gute induktive Rechtfertigungsgründe für die Annahme, dass zukünftige Theorien T_Z unsere besten gegenwärtigen Theorien T_G  früher oder später ersetzen werden. Im Lichte der Theorien Tz wird sich zeigen, dass unsere jetzigen Theorien T_G nicht wahr sind respektive nicht referieren.

"Laudans Liste" zählt einige der zurückgewiesenen Theorien T_V auf:

§ die Kristallsphären der antiken und mittelalterlichen Astronomie

§ die humorale Theorie der Medizin ("Säftelehre")

§ Die Fluidumstheorie der statischen Elektrizität
§ Die Katastrophoismustheorie der Geologie
§ die Phlogiston-Theorie der Chemie
§ die kalorische Theorie Wärme
§ die Vibrationstheorie der Wärme
§ die Vitalkräftetheorie der Physiologie
§ der elektromagnetische Äther
§ der optische Äther
§ Die Trägheitstheorie des Galileo Galilei
§ die Theorien der spontanen Generation

Diese Liste enthält einige wissenschaftliche Theorien, die einst als erfolgreich galten, sich aber als falsch herausgestellt haben. Nach Laudan spricht das erstens gegen den wissenschaftlichen Realismus im Allgemeinen, denn qua Induktion folgt, dass auch die meisten heute als erfolgreich geltenden Theorien falsch sind.

Zweitens spricht die Liste gegen das No-Miracle Argument im Speziellen. Denn die Wahrheit der Theorien auf dieser Liste war einst die beste Erklärung für ihren Erfolg. Sie ist nach heutigem Kenntnisstand aber nicht die zutreffende Erklärung.

Die Pessimistische Meta-Induktion speziell als ein Einwand gegen das No-Miracle Argument kann also als eine reductio ad absurdum rekonstruiert werden:

A1. Das No-Miracle Argument besteht in einer Inferenz von dem empirischen Erfolg wissenschaftlicher Theorien auf ihre wortwörtliche Wahrheit.

A2. Laudans Liste zeigt, dass der empirische Erfolg einer Theorie kein zuverlässiger Indikator für die Wahrheit dieser Theorie ist.

K1. Die Inferenz vom empirischen Erfolg reifer wissenschaftlicher Theorien auf ihre Wahrheit ist ungerechtfertigt. Das NMA ist also kein gutes Argument.

Es lassen sich also zwei Versionen des PMI-Argumentes unterscheiden:

1. induktive Version

2. deduktive Version

Die erste Version wird nachstehend einer Kritik unterzogen.

Das PMI als induktives Argument ist im Kern eine induktive Verallgemeinerung:

P1. Die meisten erfolgreichen Theorien haben sich als falsch erwiesen.

C1. Also: Die meisten (gegenwärtig) erfolgreichen Theorien werden sich als falsch erweisen.

Als induktive Verallgemeinerung hat das Argument die Form:

P. X% aller bisher n beobachteten Fs sind Gs.
C. Also: X% aller Fs sind Gs.

Ein solches Schluss kann nur unter zwei Bedingungen rational sein:[1]

a. Wenn es eine "natürliche Verbindung" zwischen einem F-sein und einem G-sein gibt.

b. Wenn die induktive Basis groß und repräsentativ ist.

Beide Bedingungen sind für das PMI als induktive Verallgemeinerung nicht erfüllt. Es folgt, dass das PMI als induktive Verallgemeinerung kein rationaler Schluss ist.

Erstens ist Bedingung (a) klarerweise nicht erfüllt. Denn es besteht keine "natürliche Verbindung" zwischen eine erfolgreiche Theorie sein und falsch sein.

Zweitens ist die Bedingung (b) nicht erfüllt. Die in den Prämissen eines induktiven Argumentes angeführten n beobachteten Fs bilden eine Stichprobe. Bedingung (b) sagt nun aus, dass diese Strichprobe eine gute Grundlage für eine Verallgemeinerung ist, wenn sie zum einen sehr groß und zum anderen  reprä-sentativ ist. Das kann dadurch gewährleistet werden, indem zum einen häufig  und zum anderen zufällig Fs beobachtet werden. Somit hat jedes Individuum in der Gesamtklasse aller Fs die gleiche Chance, in die Stichprobe zu langen.

Die Theorien in "Laudans Liste" bilden nun zum einen keine große Stichprobe. Und zum anderen, was noch wichtiger ist, sie wurden nicht zufällig ausgewählt. Laudan hat sie vielmehr deshalb ausgewählt, weil sie erfolgreich waren, aber falsch sind. Seine Liste ist eine voreingenommene Stichprobe und bildet keine gute keine induktive Grundlage. Seungbae Park geht hier sogar noch weiter:

„The pessimistic induction is a fallacy of biased statistics. The pessimistic inducer took samples only from science before the twentieth century. [...] The minimum requirement for fair samples is that they be randomly selected from the sciences of both before and after the year 1900. Laudan’s samples do not meet this requirement.“
- Seungbae Park: A Confutation of the Pessimistic Induction
[kursive Hervorhebung von mir]

Aber wie könnte eine bessere induktive Grundlage aussehen? Moti Mizrahi ist wie folgt vorgegangen:[2] Er hat auf der Website "Oxford Reference Online" in verschiedenen Wörterbüchern nach dem Begriff "Theorie" gesucht. Nachdem er 124 Instanzen des Begriffs "Theorie" gesammelt hatte, wählte er mit einem Zufallsgenerator 40 unter ihnen aus. Die so gewonnene Stichprobe teilte er nun schließlich in drei Kategorien ein: akzeptiert, zurückgewiesen und wird diskutiert.

Hier sein Ergebnis:

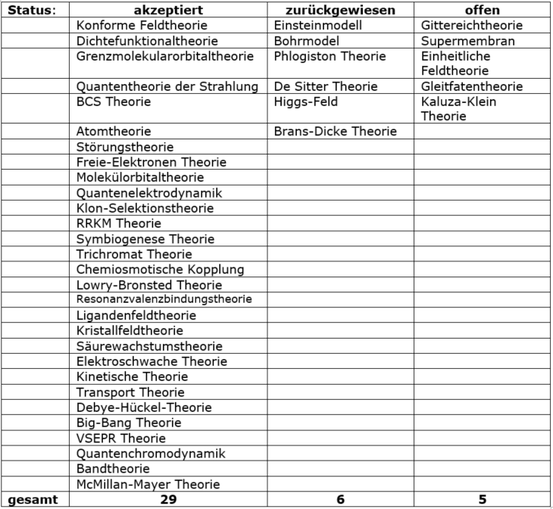
Mizrahi hat dasselbe noch einmal mit dem Begriff "Gesetz" gemacht und ein ähnliches Ergebnis bekommen. Seine Stichprobe ist auf jeden Fall größer und repräsentativer (im Sinne von: die Theorien wurden zufälliger ausgewählt[]) als die von Laudan. Eine pessimistisch-induktive Verallgemeinerung auf ihrer Grundlage würde so aussehen:

P1. 15% der Theorien in "Mizrahis Liste" wurden zurückgewiesen.

K1. 15% aller Theorien werden einmal zurückgewiesen.

Mizrahis Liste bildet keine gute Grundlage für eine "pessimistische Induktion". Mehr schon scheint sie eine "optimistische Induktion" (OMI) zu rechtfertigen:

P1. 70% der Theorien in "Mizarhis Liste" werden als wahr angesehen.

K1. Also: 70% aller Theorien werden auch in Zukunft als wahr angesehen.

Ich möchte hier aber auch keine OMI verteidigen. Meine Kritikpunkte sind vielmehr folgende: Erstens, Laudans Liste ist keine gute induktive Grundlage für  das PMI-Argument. Insbesondere stützt sie nur die Annahme P2* und nicht P2:

P2*. Einige Theorien Tv haben sich als falsch erwiesen.

P2. Die meisten Theorien Tv haben sich als falsch erwiesen.

Zweitens, es ist überhaupt nicht klar, ob eine bessere induktive Grundlage P2 stützen würde. Mizarhis Liste deutet hier in eine andere Richtung.

Drittens, selbst wenn wir eine sehr gute induktive Grundlage hätten und diese P2 stützen würde, ist überhaupt nicht einsichtig, warum das C1 rechtfertigen sollte.

Sehen wir uns dazu ein anderes induktives Argument an:

P2. Die meisten meiner bisherigen Kinder sind Mädchen.
C1. Die meisten meiner zukünftigen Kinder werden Mädchen sein.

Hier wird die Konklusion nicht von der Prämisse gestützt, selbst wenn diese de facto wahr ist. Denn dass die meisten meiner bisherigen Kinder Mädchen waren, erhöht schlichtweg nicht die Wahrscheinlichkeit dafür, dass die meisten meiner zukünftigen Kinder Mädchen sein werden. Ähnlich verhält es sich mit dem PMI-Argument. Das heißt selbst wenn die meisten Theorien Tv sich als falsch erwiesen haben, ist überhaupt nicht ersichtlich, warum es deshalb wahrscheinlicher sein sollte, dass auch in Zukunft sich die meisten Theorien als falsch erweisen werden.

[1] Peter Godfrey-Smith: Induction, Samples, and Kinds. (2011), S. 39

[2] Moti Mizrahi: The pessimistic induction: a bad argument gone too far (2013)

Für weitere (aber mMn weniger überzeugende) Kritiken am PMI siehe:

Ludwig Fahrbach: Das Argument des expotentiellen Wachstums

Philip Kitcher: Das Argument der stabilden Kausalreferenz

Samuel Rumkorff: Das Argument der Eliminativen Inferenz

zum vorherigen Blogeintrag                                        zum nächsten Blogeintrag 

Blogreihe: Wissenschaftlicher Realismus